In micromagnetics, magnetisation dynamics are described using the LLG equation. For non-zero temperature simulations we can use the LLB equation which contains an additional longitudinal susceptibility effective field contribution, as well as a longitudinal damping term. Other equations available in Boris include stochastic versions of these equations, as well as magnetisation dynamics equations complemented by spin-transfer torques and spin-orbit torques. Additionally Boris allows calculations of various spin torques in single and multi-layered geometries using a self-consistent spin transport solver (see Spin Transport).

The LLG equation is given as (for definitions of parameters refer to the manual):

(1)   \begin{equation*} \frac{\partial \mathbf{m}} {\partial t} = -\gamma \mathbf{m} \times \mathbf{H_{eff}} + \alpha \mathbf{m} \times \frac{\partial \mathbf{m}} {\partial t} \end{equation*}

In addition to external magnetic fields, a number of contributions can be included in the effective field Heff, the most commonly used are given below.

Demagnetising field:

(2)   \begin{equation*} \mathbf{H}(\mathbf{r_0}) = -\int \limits_{\mathbf{r} \in V}\mathbf{N(r - r_0) M(r)} d\mathbf{r}\end{equation*}

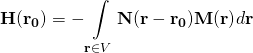
Direct exchange interaction:

(3)   \begin{equation*} \mathbf{H}=\frac{2A}{\mu_0 M_s^2} \nabla^2\mathbf{M}\end{equation*}

Dzyaloshinskii-Moriya bulk exchange interaction:

(4)   \begin{equation*} \mathbf{H}=-\frac{2D}{\mu_0 M_s^2} \nabla \times \mathbf{M} \end{equation*}

Interfacial Dzyaloshinskii-Moriya exchange interaction:

(5)   \begin{equation*} \mathbf{H}= -\frac{2D}{\mu_0 M_s^2} \left( \frac{\partial M_z}{\partial x}, \frac{\partial M_z}{\partial y}, -\frac{\partial M_x}{\partial x} - \frac{\partial M_y}{\partial y} \right)\end{equation*}

Surface exchange in multi-layered geometries:

(6)   \begin{equation*} \mathbf{H_i} = \frac{J_1}{\mu _0 M_s \Delta} \mathbf{m_j} + \frac{2J_2}{\mu _0 M_s \Delta} (\mathbf{m_i}. \mathbf{m_j})\mathbf{m_j} \end{equation*}

Uniaxial magneto-crystalline anisotropy:

(7)   \begin{equation*} \mathbf{H} = \frac{2K_1}{\mu_0 M_s} (\mathbf{m.e_A})\mathbf{e_A} + \frac{4K_2}{\mu_0 M_s} [1 - (\mathbf{m.e_A})^2] (\mathbf{m.e_A}) \mathbf{e_A} \end{equation*}

Cubic magneto-crystalline anisotropy:

(8)   \begin{equation*} \begin{align*}\mathbf{H} = -\frac{2K_1}{\mu_0 M_s} [\mathbf{e_1} \alpha (\beta ^2 + \gamma ^2) + \mathbf{e_2} \beta (\alpha ^2 + \gamma ^2) + \mathbf{e_3} \gamma (\alpha ^2 + \beta ^2) ] \\ -\frac{2K_2}{\mu_0 M_s} [\mathbf{e_1}\alpha \beta^2\gamma^2+ \mathbf{e_2}\alpha^2\beta\gamma^2+ \mathbf{e_3}\alpha^2\beta^2\gamma] \end{align*} \end{equation*}