Spin torques included in the magnetisation dynamics equation can be computed self-consistently using a drift-diffusion model. Within this model the charge and spin current densities are given as:

(1)   \begin{equation*} \mathbf{J_C} = \sigma \mathbf{E}+\beta _D D_e \frac{e}{\mu _B} (\nabla \mathbf {S}) \mathbf {m}+\theta _{SHA} D_e \frac{e}{\mu _B} \nabla \times \mathbf {S} \end{equation*}

(2)   \begin{equation*} \mathbf{J_S} = -\frac{\mu _B}{e} P \sigma \mathbf{E} \otimes \mathbf{m} - D_e \nabla \mathbf{S} + \theta _{SHA}\frac{\mu _B}{e}\boldsymbol{\varepsilon}\sigma \mathbf{E} \end{equation*}

Here JS is a rank-2 tensor such that JSij signifies the flow of the j component of spin polarisation in the direction i. Equation (2) contains contributions due to i) drift included in ferromagnetic (F) layers, where P is the current spin-polarisation and s the electrical conductivity, ii) diffusion, where De is the electron diffusion constant, and iii) spin-Hall effect, included in non-magnetic (N) layers, where \theta _{SHA} is the spin-Hall angle and \boldsymbol{\varepsilon} is the rank-3 unit antisymmetric tensor. Equation (1) contains contributions due i) Ohm’s law, ii) CPP-GMR in multilayers , and iii) inverse spin-Hall effect. The spin accumulation, S, satisfies the equation of motion:

(3)   \begin{equation*} \frac{\partial \mathbf{S}} {\partial t} = -\nabla . \mathbf{J_S} - D_e \left(\frac{\mathbf{S}}{\lambda _{sf} ^2} + \frac{\mathbf{S \times m}}{\lambda _{J} ^2} + \frac{\mathbf{m \times (S \times m)}}{\lambda _{\phi} ^2} \right) \end{equation*}

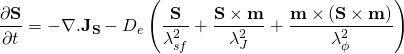
For boundaries containing an electrode with a fixed potential, differential operators applied to V use a Dirichlet boundary condition. For other external boundaries we require both the charge and spin currents to be zero in the direction normal to the boundary, i.e. JC.n = 0 and JS.n = 0. This results in the following non-homogeneous Neumann boundary conditions:

(4)   \begin{equation*} \nabla V.\mathbf{n}=\theta _{SHA}\frac{D _e}{\sigma}\frac{e}{\mu _B}(\nabla \times \mathbf{S}).\mathbf{n}\end{equation*}

(5)   \begin{equation*} (\nabla \mathbf{S}).\mathbf{n}=\theta _{SHA}\frac{\sigma}{D_e}\frac{\mu _B}{e} (\boldsymbol{\varepsilon}\mathbf{E}).\mathbf{n}\end{equation*}

At the interface between two N layers we obtain composite media boundary conditions for V and S by requiring both a potential and associated flux to be continuous in the direction normal to the interface, i.e. V and JC, and S and JS respectively. At an N/F interface we do not assume such continuity, but instead model the absorption of transverse spin components using the spin-mixing conductance:

(6)   \begin{equation*} \mathbf{Jc.n}|_N = \mathbf{Jc.n}|_F = -(G^{\uparrow} + G^{\downarrow})\Delta V + (G^{\uparrow} - G^{\downarrow})\Delta \mathbf{V_S.m} \end{equation*}

(7)   \begin{equation*} \mathbf{Js.n}|_N - \mathbf{Js.n}|_F = \frac{2 \mu _B}{e} \left[ Re{G^{\uparrow \downarrow}} \mathbf{m} \times (\mathbf{m} \times \Delta \mathbf{V _S}) + Im{G^{\uparrow \downarrow}} \mathbf{m} \times \Delta \mathbf{V _S} \right] \end{equation*}

(8)   \begin{equation*} \mathbf{Js.n}|_F = \frac{\mu _B}{e} \left[-(G^{\uparrow} + G^{\downarrow}) (\Delta \mathbf{V _S} . \mathbf{m}) \mathbf{m} + (G^{\uparrow} - G^{\downarrow}) \Delta V \mathbf{m} \right] \end{equation*}

Here \Delta V is the potential drop across the N/F interface (\Delta V = V _F - V _ N) and \Delta \mathbf{V _S} is the spin chemical potential drop, where \mathbf{V_S} = (D_e / \sigma)(e / \mu _B) \mathbf{S} , and G^\uparrow, G^\downarrow are interface conductances for the majority and minority spin carriers respectively. The transverse spin current absorbed at the N/F interface results in a torque on the magnetisation as a consequence of conservation of total spin angular momentum. If the F layer has thickness dF, this interfacial torque is obtained as:

(9)   \begin{equation*} \mathbf{T_S} = \frac{g \mu _B}{e d_F}\left[Re{G^{\uparrow \downarrow}} \mathbf{m} \times (\mathbf{m} \times \Delta \mathbf{V _S}) + Im{G^{\uparrow \downarrow}} \mathbf{m} \times \Delta \mathbf{V _S} \right] \end{equation*}

Bulk spin torques are obtained as:

(10)   \begin{equation*} \mathbf{T_S} = -\frac{D_e}{{\lambda _J}^2}\mathbf{m} \times \mathbf{S} - \frac{D_e}{{\lambda _{\phi}}^2}\mathbf{m} \times (\mathbf{m} \times {\mathbf{S}}) \end{equation*}

In the equation of motion for m, these torques are included as:

(11)   \begin{equation*} \frac{\partial \mathbf{m}} {\partial t} = -\gamma \mathbf{m} \times \mathbf{H_{eff}} + \alpha \mathbf{m} \times \frac{\partial \mathbf{m}} {\partial t} + \frac{1}{M_S}\mathbf{T_S}\end{equation*}

Using the composite media boundary conditions above we can also include spin pumping on the N side of the equation as:

(12)   \begin{equation*} \mathbf{J_S}^{pump} = \frac{\mu _B \hbar}{e^2} \left[ Re{G^{\uparrow \downarrow}} \mathbf{m} \times \frac{\partial \mathbf{m}} {\partial t} + Im{G^{\uparrow \downarrow}} \frac{\partial \mathbf{m}} {\partial t} \right]\end{equation*}